数理論理学からの
『型システム入門』入門？

@FP_Matsuri2025, 2025/06/15

自己紹介

name: Motoki Shakagori
screenName: ほとけ
org: 株式会社ベースマキナ
firstProgrammingLanguage: OCaml

https://linktr.ee/mshaka

Introduction

Introduction

『型システム入門』の難しさ

  • 数学的な素養が求められる
  • 気持ちをしっかり理解していないと迷子になりやすい
Introduction
朗報
Introduction

だいたい論理学から学べる

  • 型というアイデア自体が論理学に由来
  • 手法もかなりの部分論理学から来ている
Introduction

論理学と型システム理論の類似性

論理学 型システム
意味の世界 意味論 操作的意味論
証明の世界 証明論 型システム
2つの関係 健全性・完全性 型安全性（健全性）
Introduction

発表の流れ

  1. 論理学の話
  2. 型システムの話
  3. まとめ

1. 論理学の基礎

論理学の基礎

論理学の仕事

  • まともな推論とそうでない推論の線引き
  • 推論: いくつかの前提から、1つの結論を導くこと
論理学の基礎

推論の具体例

前提1 雨が降っている
前提2 私は傘を持っている

結論  雨が降っている、かつ私は傘を持っている
論理学の基礎

論理学の2つの流儀

まともな推論の基準を定めるのに、以下の二つの流儀がある（以下はとりわけ古典命題論理に関する説明）

  • 意味論
    • 前提が全て真であるとき結論も真ならばその推論はまとも。推論が「妥当」とも呼ぶ。真/偽が意味
  • 証明論
    • 前提にいくつかの規則を有限回適用して結論を導くことができたらその推論はまとも。そのとき前提から結論が「証明できる」とか「導出できる」とも呼ぶ
論理学の基礎

意味論

前提が全て真であるような状況を考える。先ほどの具体例を使えば

  • 「雨が降っている」を, 「私は傘を持っている」をとする
  • 結論はと書く
  • とが真であるとき、も真なので、この推論は妥当
𝑃𝑄𝑃∧𝑄TTTTFFFTFFFF
論理学の基礎
  • その他の論理演算子を使った文についても真偽値を割り当てられる
  • 真偽値の割り当て方は、数学の議論における常識的な用法を踏襲している
𝑃¬𝑃TFFT𝑃𝑄𝑃∧𝑄𝑃∨𝑄𝑃→𝑄TTTTTTFFTFFTFTTFFFFT
論理学の基礎

証明論

「前提にいくつかの規則を有限回適用して結論を導く」（再掲）

  • とが真か偽かは考えない
  • 「とが証明済みとして与えられたら、そのままも証明可能」としていいという発想
  • 証明済みの前提から、特定の結論を導けることを約束する規則を定める（導出規則）
論理学の基礎

導出規則の例

自然演繹と呼ばれる体系の導出規則の抜粋

𝑃𝑄∧𝐼𝑃∧𝑄𝑃∧𝑄∧𝐸1𝑃𝑃∧𝑄∧𝐸2𝑄𝑃∨𝐼1𝑃∨𝑄𝑄∨𝐼2𝑃∨𝑄𝑃∨𝑄[𝑃]:𝑅[𝑄]:𝑅∨𝐸𝑅[𝑃]:𝑄→𝐼𝑃→𝑄𝑃→𝑄𝑃→𝐸𝑄
論理学の基礎

証明の例

からを導く証明

[𝑃∧(𝑄∧𝑅)]∧𝐸1𝑃[𝑃∧(𝑄∧𝑅)]∧𝐸2𝑄∧𝑅∧𝐸1𝑄∧𝐼𝑃∧𝑄[𝑃∧(𝑄∧𝑅)]∧𝐸2𝑄∧𝑅∧𝐸2𝑅∧𝐼(𝑃∧𝑄)∧𝑅
論理学の基礎

何が嬉しいのか？

  • 意味を考えずに記号に対する操作だけ考えればいいので純粋
  • 証明という数学者の営みを、有限で誰にでもわかるかたちで（？）数学的に記述できる
  • 有限な記号に対して機械的に規則を適用していくだけなので、ある文が証明可能であることを機械的に検査できる（プログラムのように）
  • 部分的な証明にどんどん分解されていき、いつかは止まる
論理学の基礎

健全性と完全性

  • 証明に使える規則をうまく定義すると、意味の世界とのある関係が成り立つ
  • 健全性 (soundness): 証明可能なら妥当（変な結論を出さないか）
  • 完全性 (completeness): 妥当なら証明可能（十分な証明力を持つか）
  • 古典命題論理以外にもさまざまな論理があるが、他の論理の研究でも健全性と完全性が示されている
論理学の基礎

論理学まとめ

  • 論理学は、推論の妥当性を数学的に記述する学問
  • 論理学には、意味と証明の2つの世界がある
  • 証明体系を評価する指標としての健全性と完全性

2. 型システムって何？

型システムって何？

インフォーマルな定義

型システムは、プログラムをなんらかの仕方で分類することによって、プログラムが望ましくない振る舞いを起こさないことを保証する仕組み

型システムって何？

必要な議論

  1. プログラムの振る舞いを定める（操作的意味論）
  2. プログラムの分類の仕方を定める（型システム）
  3. 「望ましくない振る舞いを起こさないことを保証」できていることの確認（型安全性）
型システムって何？

ところで、
みなさんは型付きラムダ計算を……

型システムって何？

知っていますね😊

型システムって何？

題材とするプログラミング言語

  • 今後の説明では型付きラムダ計算にブール値と条件式を加えた言語を使う
  • 今後は単に「ラムダ計算」といえばこの言語を指すものとする
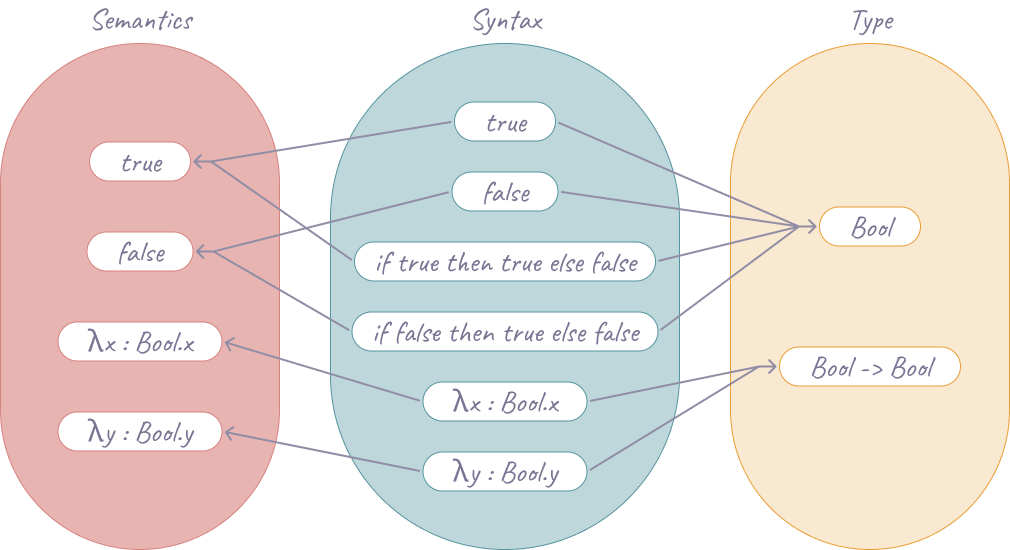
  • 以下は構文定義
t ::= true | false（ブール値）
    | if t then t else t（条件式）
    | x （変数）
    | λx:T.t （ラムダ抽象。Haskellなら単に`\x -> t`。`T`は型で、説明の都合上たまに省略する）
    | t t （適用。要するに関数の呼び出し）
型システムって何？

プログラムの振る舞い

型システムって何？
  • 振る舞いは、要するに「プログラムがどのように評価されるか」ということ
  • （値呼びの）高級な言語なら
    • 1 + 1という式は2に評価される
    • f(1 + 1)ならまず引数を評価するので、f(2)になる
  • こういう評価規則を定める議論を操作的意味論と呼ぶ
型システムって何？

ラムダ計算の操作的意味論（インフォーマル・抜粋版）

  • はそれ以上評価できない
  • はに評価される
  • はに評価される
  • はまず、そのあとに評価される

どんどん評価していくと最終的に, , あるいはラムダ抽象になる

型システムって何？

ラムダ計算の操作的意味論（フォーマル・完全版）

矢印は「評価可能」、横棒は「上段が成り立っていれば下段も成り立つ」と読む

t1→t′1E-App1t1 t2→t′1 t2t2→t′2E-App2v1 t2→v1 t′2E-AppAbs(𝜆x.t12) v2→[x↦v2]t12
  • E-App1: 関数適用の左辺が評価できるなら評価する
  • E-App2: 関数適用の右辺が評価できるなら評価する
  • E-AppAbs: 関数適用の左辺がラムダ抽象で右辺が値なら、右辺をラムダ抽象の本体に代入する
型システムって何？
E-IfTrueif true then t2 else t3→t2E-IfFalseif false then t2 else t3→t3t1→t′1E-Ifif t1 then t2 else t3→if t′1 then t2 else t3
  • E-IfTrue: 条件式の条件がtrueなら、条件式の真の方を評価する
  • E-IfFalse: 条件式の条件がfalseなら、条件式の偽の方を評価する
  • E-If: 条件式の条件が評価できるなら評価する
型システムって何？

望ましくない振る舞い

  • は評価できない
    • に値を適用する規則を定義していない
  • （JavaScriptですらここでランタイムエラーになる）
  • 典型的には、このような評価が定義されていないプログラムが望ましくない
型システムって何？

プログラムを分類する

  • さきほどの例では、が適用の左辺に来てしまうのがよくなかった
  • これを評価する前に検知するため、式がとりうる値の種類に応じて分類する
  • 値の種類を表すラベルが型
    • 「最終的にラムダ抽象になります」というラベルがついていたら🙆‍♀️
    • それ以外のラベルがついていたら🙅‍♀️

➡️証明論と同じように、型の導出規則というものを定める

型システムって何？

基本的なアイデア

  • , : 直観的に真偽値っぽいので、真偽値型の気持ちでというラベル（型）を与えてよさそう
  • : の戻り値の型になりそう
    • ただし、がラムダ抽象であり、の型がその引数と一致している必要がある
  • : 戻り値の型はが型であるときのの型と一致しそう
  • （変数）: それ自体では情報が足りないのでなんらかの前提が必要
    • 典型的にはラムダ抽象の中にあるので引数の型アノテーションに依存しそう like
型システムって何？

型付けの導出規則

T-VarΓ,x:T⊢x:TΓ,x:T1⊢t2:T2T-AbsΓ⊢𝜆x:T1.t2:T1→T2Γ⊢t1:T11→T12Γ⊢t2:T11T-AppΓ⊢t1 t2:T12T-TrueΓ⊢true:BoolT-FalseΓ⊢false:BoolΓ⊢t1:BoolΓ⊢t2:TΓ⊢t3:TT-IfΓ⊢if t1 then t2 else t3:T
型システムって何？

型付けの導出図の例

の型付け導出図。こういう図が書けることを「型付け可能」と呼ぶ

T-Varx:Bool⊢x:BoolT-Abs⊢𝜆x:Bool.x:Bool→BoolT-True⊢true:BoolT-App⊢(𝜆x:Bool.x)true:Bool
型システムって何？

型システムは証明の世界

  • 型の導出でも証明論と同じような図が生えた
  • これも有限なかたちで表された証明図と考えることができる
    • 部分プログラムに遡って型をつけて行くので（うまく定義すれば）いつかは停止する
  • 証明体系と同様に、プログラムが型付け可能か否かを機械的に判定可能（なように作られている）
型システムって何？

型安全性

  • 「望ましくない振る舞いが起こらないこと」が保証できているか？
  • （インフォーマルには）「プログラムが型付け可能なら、そのプログラムには望ましくない振る舞いが起こらない」ような型システムを安全と呼ぶ
  • 論理学の健全性（「証明可能なら妥当」）に対応し、型システムについても健全と呼ぶことがある
型システムって何？

（補足）ラムダ計算の操作的意味論と型の導出の規則って似てない？

  • 評価した値もプログラムの分類として使えると言えばそう
  • 型システムの方が（概して）分類として荒く計算量的に扱いやすい

3. まとめ

まとめ

謎の表again

論理学 型システム
意味の世界 意味論 操作的意味論
証明の世界 証明論 型システム
2つの関係 健全性・完全性 型安全性（健全性）
まとめ

なぜ論理学を学ぶとよいのか

  • 型システムのベースとなるアイデア・気持ちがわかる
  • （発表の内容と関係ないけど）
    • 帰納法を使った証明に慣れることができる
    • 論理学の方が教材が多い
まとめ

Thank you!